


Last Update: Fri Aug 12 20:12 EDT 2022
My curiosity about wind turbine visibility, from the shore, and the Earth's curvature got me to thinking about it. I dusted off a little high school trigonometry and physics to check out a few things that I have been seeing in the press.
This article is not a statement pro or con about the building of wind turbines off shore, it is simply an exercise to help me think about what it might look like. It uses a scientific approach toward understanding how they would appear from the shore. None of the other important issues are addressed here.
From what I've read, the placement of the wind turbines is projected to be between 9 and 20 miles from shore. So the calculations here bracket those numbers. News reports talk about reports that the companies have written. I have not seen any of those. If I do get to see them I may make additions or changes here.
I saw a quote from one of the reports that said the turbines would be able to be seen for 40 miles.
My calculations below show that a wind turbine 1048 feet tall would completely disappear, for a 6 foot person on the beach, due to the Earth's curvature, at 42.6 miles. For an observer 50 feet above the beach, the tower would disappear at 48.3 miles.
So I find the claim above of 40 miles credible. But I show my calculations. Perhaps the reports showed their calculations also, but I don't know.
The next question to ask then, is how much of its height would be obscured at shorter distances? The same equations tell us that at the height of a six foot person, a 25 foot tower would be fully obscured by the Earth's curvature at 9.1 miles. And a 190 foot tower would be fully obscured at 20.0 miles.
This means such towers could be seen under ideal weather conditions. Curvature of the Earth only helps to obscure a little bit of wind turbines at the distances involved.
My calculations also show that a 1048 foot tower (shortened by 25 feet to be 1023 feet visible by the Earth's curvature) 9.0 miles away, would appear to a 6 foot observer to be the size of a quarter held 3.7 feet (44.4 inches) from the observer's eyes. The same tower at 20.0 miles away (shortened by 190 feet) would appear to the same observer to be the size of a quarter held 9.8 feet (117.6 inches) from the observer's eyes.
My calculations also do not include things like haze, humidity, clouds, pollution, etc. that would reduce visibility, nor possible lens like "focusing" of objects in view by things like light scattering and atmospheric effects, which I have no experience in calculating. These calculations do assume a perfectly spherical Earth, which actually is a reasonably valid approximation for the surface of a large body of water. (because water is a liquid and gravity causes it to follow the natural curvature of the Earth).
Table summaries of various calculated results:
The distance required for the Earth's curvature to fully obscure a tower of a given height:
| Viewer Height(ft) |
Tower Height(ft) |
Obscured At (miles) |
|---|---|---|
| 6.0 | 1048.0 | 42.6 |
| 6.0 | 25.0 | 9.1 |
| 6.0 | 96.0 | 15.0 |
| 6.0 | 190.0 | 19.9 |
| 50.0 | 1048.0 | 48.3 |
| 50.0 | 1.2 | 10.0 |
| 50.0 | 86.0 | 20.0 |
The next question to ask, is how large the 1023 foot tower (1048 - 25) would appear when 9 miles away. A practical way to approach this question is to compute how far you would have to hold a quarter from your eyes to fully obscure the tower 9 miles away.
The answer I got is 1.1 meters (or 3.7 feet or 44.4 inches). So if you want to see how large one single 1048 foot tower will appear at 9 miles away, tape a 12" ruler to the end of a yardstick, then tape a quarter to it at 44.4 inches (so that you see the full obverse or reverse), then hold the other end of the yardstick near your eye and observe the size of the quarter against the background of the ocean, or any distant view. That will be how big the tower will appear at 9 miles away.
A table of various distances from the eye required for a quarter to fully obscure the view of a tower of a given height:
| Tower Height(ft) |
Distance to Tower((miles) |
Obscured by Earth's Curvature(ft) |
Viewable Tower Height(ft) |
Distance to Quarter(feet) |
Distance to Quarter(inches) |
|---|---|---|---|---|---|
| 1048.0 | 9.0 | 25.0 | 1023.0 | 3.7 | 44.4 |
| 1048.0 | 15.0 | 96.0 | 952.0 | 6.6 | 79.5 |
| 1048.0 | 20.0 | 190.0 | 858.0 | 9.8 | 117.6 |
Before showing the derivation of the equations, there is another point I'd like to consider regarding the quarter sized view blocking. The calculation of how far away a quarter would obscure the tower is an opaque disk blocking all visibility at all points on the disk. A tower is a slender tower, with moving stick-like blades. Although the tower may be seen, it is mostly transparent to seeing the unimpeded view. It seems that this would greatly reduce the obtrusiveness of the view, the eye-brain connection perhaps assisting.
This effect is shown here by comparing these three images, a solid quarter. a slender black wind turbine, and a slender white wind turbine:



So rather than taping a quarter to a yardstick, perhaps the better model is to take a transparent disk the size of a quarter, and draw a stick figure of a turbine on it, and hold that up at the calculated distance with the ocean in the background, and that should be close to what an observer would see.
To get a feel for the field of view at the horizon obscured by a quarter at the various distances, photographs were taken from the Ocean City boardwalk (between 17th and 18th Streets, to avoid crowds. Unfortunately, dunes now largely obscure ocean views) with a quarter mounted on a wire attached to the boardwalk railing, and camera postitions at the computed distances from the quarter and positioning the quarter at the horizon. The results are below.
The images in the left column show the opaque quarter at the horizon (seen in the gap between the dunes), the images in the middle column show the mostly transparent black wind turbine at the horizon, and the images in the right column show the mostly transparent white wind turbine at the horizon. The turbine images are placed at the position of, and scaled to the size of, the quarter in the left column. The location of the quarter or the wind turbine image is easily seen in 9.0 mile images, and is at the same location in the 15.0 and 20.0 mile images.
If you click on any one of these nine images, a full screen view of it will be shown.
![[image]](09_miles_quarter.jpg)
![[image]](09_miles_quarter_black.jpg)
![[image]](09_miles_quarter_transparent.jpg)
![[image]](15_miles_quarter.jpg)
![[image]](15_miles_quarter_black.jpg)
![[image]](15_miles_quarter_transparent.jpg)
![[image]](20_miles_quarter.jpg)
![[image]](20_miles_quarter_black.jpg)
![[image]](20_miles_quarter_transparent.jpg)
This should be a good approximation of how a single wind turbine would appear from shore, at the three distances noted. This video on youtube by Ørsted that shows their projection of what the wind farms would look like from Atlantic City (15 miles), Ocean City, and Stone Harbor. [The accompanying news article is here.] This appears to be relatively consistent with the calculations here. Their video also shows how haze, clouds, etc. would reduce or obscure the turbine view as opposed to a perfectly clear day, which is what the calculations here assume.
Now for the derivation of the required equations, and Fortran programs to do the calculations (I assure you I did the first calculations on paper with hand drawn sketches and my cell phone's calculator), and the raw computer program output.
Here is the diagram that allows one to write down the equations:
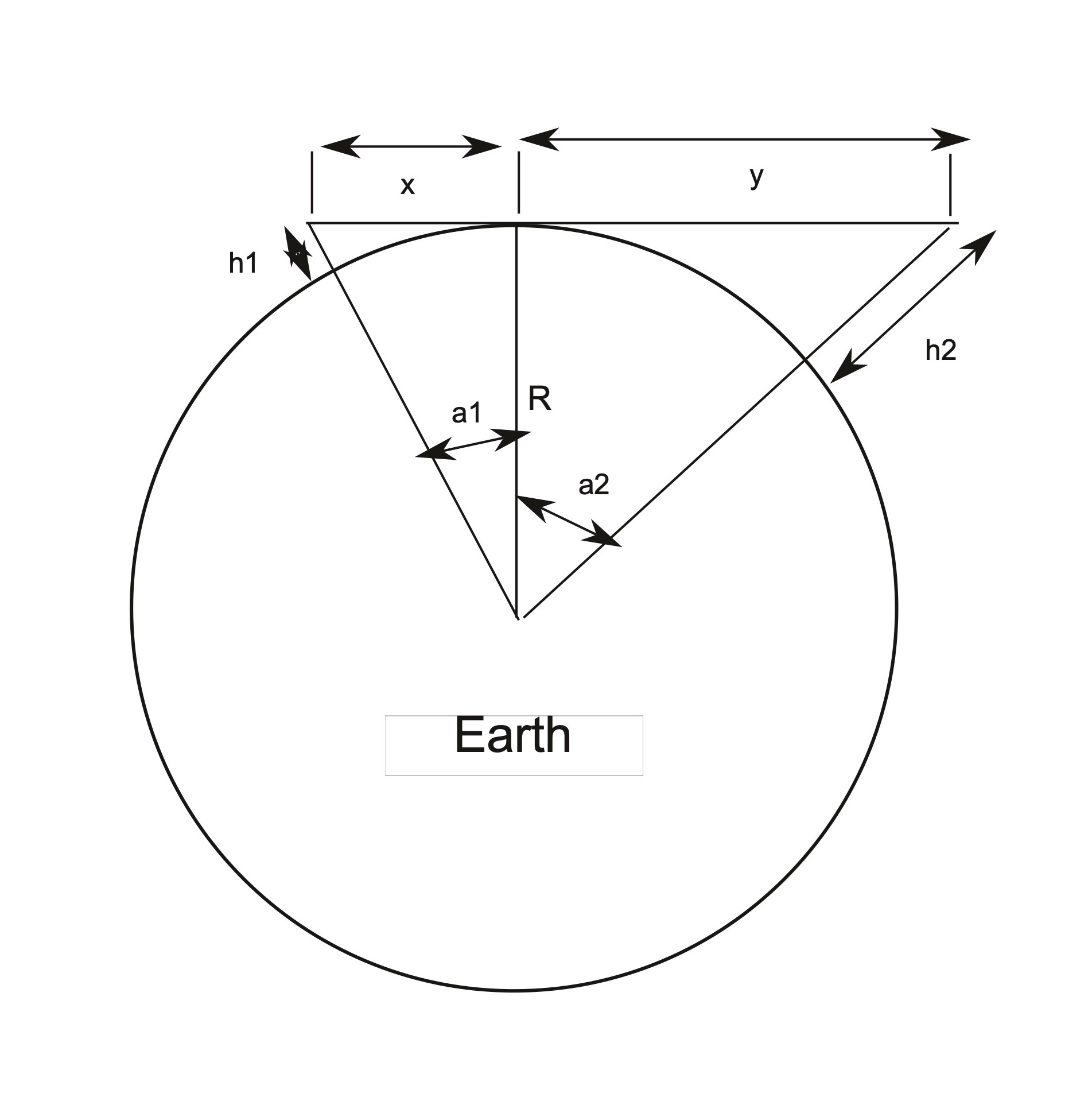
h1 = the height of the observer
h2 = the height of the tower
R = the radius of the Earth (6,371,000 meters)
C = the circumference of the Earth (=2πR)
x = the distance from the observer to the point on the Earth obscuring the full tower view
y = the distance from the point on the Earth obscuring the full tower view to the tower
a1 = the angle subtended on the Earth's surface from the observer to the point of obstruction on the Earth
a2 = the angle subtended on the Earth's surface from the point of obstruction on the Earth to the tower
ds = the curved surface Earth distance from the observer to the tower
The equations:
The Pythagorean Theorem (the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides) gives:
(R + h1)2 = x2 + R2
(R + h2)2 = y2 + R2
Solving these for the two unknowns, x and y, gives:
x = √(h1 *(2 * R + h1))
y = √(h2 *(2 * R + h2))
The angles are given by:
tan(a1) = x/R
tan(a2) = y/R
which gives:
a1 = arctan(x/R)
a2 = arctan(y/R)
Now the total angle subtended is:
angle = a1 + a2
And with the angle in degrees, the distance along the surface, ds, can be computed as the fraction of the total 360.0 degrees being the same fraction of the circumference of the Earth as:
angle/360.0 = ds/C
Note: angle(in degrees) = angle(in radians) * 180.0 / π
giving:
ds = C * angle / 360.0
The straight line distance x + y is not the same as the curved distance, ds, as measured on the surface of the Earth where h1 and h2 touch the surface of the Earth. So after computing the two angles a1 and a2 from their tangents, the distance on the circumference of the Earth was also computed. For the distances involved here, on the surface of the Earth, to the significant number of decimal digits, the distances come out the same. Saying this mathematically: x + y = ds . So the sketch used to develop the equations is accurate, but not to scale.
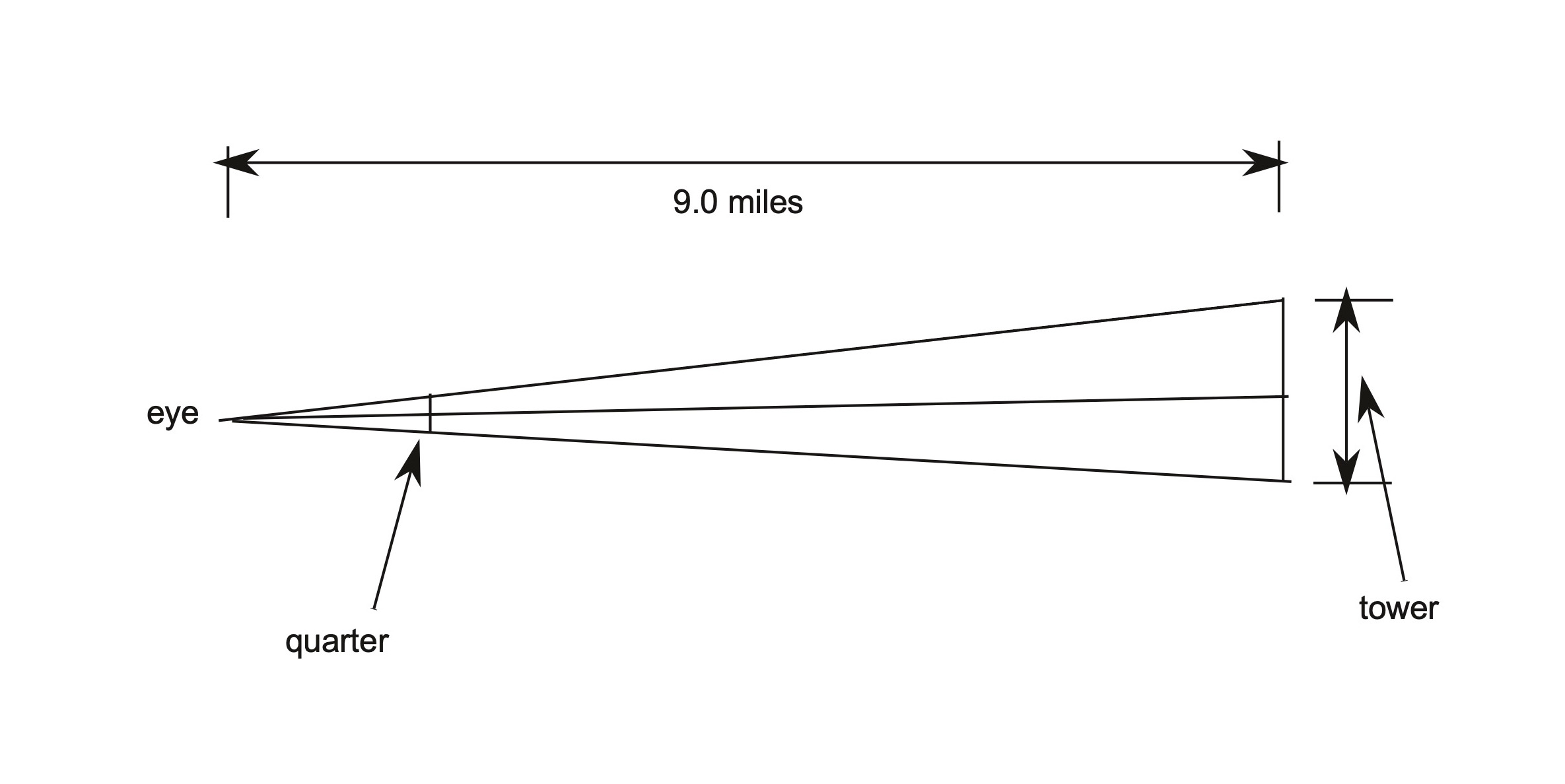
dtower = distance from the eye to the tower
dquarter = diameter of a quarter (24.26 mm)
htower = height of the tower - height of the tower obscured at distance d
dtoquarter = distance from the eye to the quarter
alpha = half of the angle of the view subtended by the tower at the given distance d
this is also equal to half of the angle of the view subtended by the quarter at the distance it will
fully obscure the tower
using half the angle allows us to base the tangent computation on a right triangle.
(these parameters aren't explicitly labeled on the diagram, but should be clear from the description)
The equations:
tan(alpha) = (htower/2.0) / dtower = htower / (2.0 * dtower)
In terms of the quarter, the same angle's tangent is:
tan(alpha) = (dquarter / 2.0) / dtoquarter = dquarter / (2.0 * dtoquarter)
Equating the two expressions for tan(alpha) we get:
htower / (2.0 * dtower) = dquarter / (2.0 * dtoquarter)
Solving this for dtoquarter gives:
dtoquarter = dquarter * (dtower / htower)
Notes: Be careful to use consistent units. The program below converts distances to meters
for the calculations, then with the result in hand, converts to also to feet and inches.
Since tan(alpha) is computed and then used directly to compute dtoquarter, one need not bother to convert
it to degrees.
Note: The above calculations are subject to the caveats:
Uniform Earth curvature over the ocean.
The observer is standing at sea level.
Full atmospheric visibility, e.g. no clouds, pollution, humidity, etc. interference.
Any atmospheric "focusing" effects (e.g. light bending or parallax) are ignored.
If I made any errors in these calculations, please let me know, but they seem to be correct.
Now for the Fortran programs that I wrote to do these calculations.
implicit double precision (a-h,o-z)
pi = 3.1415926
ampermile = 1609.34
feetpermeter = 3.28084
write(6,900)
900 format(' Wind Turbine Visibility Calculations')
c distances in meters
c Radius of the Earth
R=6371000.0
c height of a hypothetical man assumed to be 6 feet
heightman = 6.0
h1 = heightman / feetpermeter
c height of a wind turbine, here assumed to be 1048 feet (Sandpaper article 06 Jul 2022)
heightturbine = 1048.0
c heightturbine = 25.0
h2 = heightturbine / feetpermeter
write(6,800)R,h1,h2
800 format('R= ',f15.1,' meters (Radius of the Earth)',/,'h1= ',f8.1,
* ' meters (height vantage point)',/,'h2= ',
* f8.1,' meters (height of wind turbine)')
x = SQRT(h1 * (2.0 * R + h1))
write(6,803)ampermile
803 format('ampermile=',f8.1,' meters')
write(6,804)feetpermeter
804 format('feetpermeter=',f8.5,' feet')
write(6,901)x
901 format('x = ',f8.1,' meters (vantage point to tangent point)')
y = SQRT(h2 * (2.0 * R + h2))
write(6,902)y
902 format('y = ',f8.1,' meters (tangent point to wind turbine)')
xplusy = x + y
write(6,910)xplusy
910 format('x + y =',f12.1,' meters')
xplusymiles = xplusy / ampermile
write(6,911)xplusymiles
911 format('x + y =',f12.1,' miles')
tan1 = x/R
a1 = datan(tan1)
write(6,903)a1
903 format('a1=',f12.5,' radians')
a1deg = a1 * 180.0 / pi
write(6,905)a1deg
905 format('a1deg=',f9.5,' degrees')
tan2 = y/R
a2 = datan(tan2)
write(6,904)a2
904 format('a2=',f12.5,' radians')
a2deg = a2 * 180.0 / pi
write(6,905)a2deg
906 format('a2deg=',f8.1,' degrees')
c total angle in degrees
asumdeg = a1deg + a2deg
write(6,907)asumdeg
907 format('asumdeg=',f8.1,' total Earth angle subtended in degrees')
c circumference of the Earth
C = 2.0 * pi * R
write(6,802)C
802 format('C=',f12.1,' meters (circumference of Earth)')
d = C * asumdeg /360.0
write(6,908)d
908 format('d=',f12.1,
* ' meters (distance from vantage point to wind turbine',
* ' over curved Earth)')
dmiles = d / ampermile
write(6,909)dmiles
909 format('dmiles=',f8.1,
* ' miles (distance from vantage point to wind turbine',
* ' over curved Earth)')
write(6,912)heightman,heightturbine,dmiles
912 format('vantage point height=',f4.1,' feet,',' turbine height=',
* f7.1,' feet, ',' obscured at',f6.1,' miles')
call exit
end
OUTPUT:
Wind Turbine Visibility Calculations
R= 6371000.0 meters (Radius of the Earth)
h1= 1.8 meters (height vantage point)
h2= 319.4 meters (height of wind turbine)
ampermile= 1609.3 meters
feetpermeter= 3.28084 feet
x = 4827.3 meters (vantage point to tangent point)
y = 63798.8 meters (tangent point to wind turbine)
x + y = 68626.1 meters
x + y = 42.6 miles
a1= 0.00076 radians
a1deg= 0.04341 degrees
a2= 0.01001 radians
a1deg= 0.57374 degrees
asumdeg= 0.6 total Earth angle subtended in degrees
C= 40030171.7 meters (circumference of Earth)
d= 68623.9 meters (distance from vantage point to wind turbine over curved Earth)
dmiles= 42.6 miles (distance from vantage point to wind turbine over curved Earth)
vantage point height= 6.0 feet, turbine height= 1048.0 feet, obscured at 42.6 miles
Summary of running the program with other values of interest:
Turbine:
vantage point height= 6.0 feet, turbine height= 1048.0 feet, obscured at 42.6 miles
vantage point height= 6.0 feet, turbine height= 25.0 feet, obscured at 9.1 miles
vantage point height= 6.0 feet, turbine height= 96.0 feet, obscured at 15.0 miles
vantage point height= 6.0 feet, turbine height= 190.0 feet, obscured at 19.9 miles
vantage point height=50.0 feet, turbine height= 1048.0 feet, obscured at 48.3 miles
vantage point height=50.0 feet, turbine height= 1.2 feet, obscured at 10.0 miles
vantage point height=50.0 feet, turbine height= 86.0 feet, obscured at 20.0 miles
implicit double precision (a-h,o-z)
pi = 3.1415926
ampermile = 1609.34
feetpermeter = 3.28084
write(6,900)
900 format(' Wind Turbine Perspective Calculation')
dtower = 9.0
dtowerm = dtower * ampermile
write(6,300)dtower,dtowerm
300 format('dtower=',f8.1,' miles',f12.1,' meters')
htower = 1048.0 - 25.0
htowerm = htower / feetpermeter
write(6,301)htower,htowerm
301 format('htower=',f8.1,' feet ',f8.1,' meters')
dquarter = 24.26
dquarterm = dquarter / 1000.0
write(6,302)dquarter,dquarterm
302 format('dquarter=',f8.1,' mm',f12.4,' meters')
dtoquarterm = dquarterm * (dtowerm / htowerm)
dtoquarterf = dtoquarterm * feetpermeter
dtoquarteri = dtoquarterf * 12.0
write(6,305)htower,dtower,dtoquarterm,dtoquarterf,dtoquarteri
305 format('htower=',f8.1,' feet ','dtower=',f8.1,' miles: ',
* 'dtoquarter=',f8.1,' meters',f8.1,' feet',f8.1,' inches')
call exit
end
OUTPUT:
Wind Turbine Perspective Calculation
dtower= 9.0 miles 14484.1 meters
htower= 1023.0 feet 311.8 meters
dquarter= 24.3 mm 0.0243 meters
htower= 1023.0 feet dtower= 9.0 miles: dtoquarter= 1.1 meters 3.7 feet 44.4 inches
Summary of running the program with other values of interest:
Perspective:
htower= 1023.0 feet dtower= 9.0 miles: dtoquarter= 1.1 meters 3.7 feet 44.4 inches
htower= 952.0 feet dtower= 15.0 miles: dtoquarter= 2.0 meters 6.6 feet 79.5 inches
htower= 858.0 feet dtower= 20.0 miles: dtoquarter= 3.0 meters 9.8 feet 117.6 inches